实现一个 ECMAScript Parser 需要做的事情

Grater 目前在比较初期的阶段，代码已开源，可以在这里体验

Hi，首先在开始之前，我得承认，我并没有 CS 教育的经历。通常这句话的后面一定有转折语句，我想这里还是不要有了。所以虽参考多个领域内概念，但落地总体还是偏向于实用主义。

在专注前端一段时间后，可能会发现工具链中有很多都包含基础的 Parser，比如 TypeScript 的

Parser，React 使用的 Parser 是 Acorn 以及 Acorn-JSX ，之前是使用 Esprima 的 fork 版本，ESLint 也是一样，只是改了名字叫 Espree，而 Babel 使用了自己的 Parser。

可能会有个疑惑是为什么不利用 Lex/Yacc 来快速实现，而是选择 CP 值有些低的手写方式。有实现一个 JS AST Parser 的想法来自于 “我想与 JS 更近一点”，很难描述这种情感，通常人们可能普遍认为这是一种自我描述性质的解释。在这个过程中看了很多类型的 Parser 实现，由衷感谢这些开源巨人们，没有这些作为参考，绝对没有这篇文章以及 Grater。

Grater 是一个输出符合 ESTree 定义结构 AST 的 ECMAScript Parser，目前基本实现了大部分 ES5 所包含的定义，初期大目标是追上最新 ES 标准实现。在输入符合语法规则的代码前提下，解析出 AST，没有做 Tokens 的输出（也是因为 Tokens 并没有一个官方规范标准），以及更加复杂的错误恢复机制

使用 TS 来书写 Grater 是为了尽量减少一些心智负担，能够预想到这个项目不会很小，增加一些必要的约束可以提高效率，也能利用 ES-Tree 的类型定义完善结构

实现一个最普世的 AST Parser，流程如下：

SourceCode ~~ Tokenizer ~~> Token Stream ~~ Parsing ~~> AST

简要来说，源码将被 Tokenizer 后形成 一长串不同类型的 Token 字节流，以便于我们按照规范的定义，在 Parsing 阶段解析相应的语法语句结构，形成特定的 AST 结构。

我们目标是产生符合标准的 AST，也就是要符合 The ESTree Spec，而解析方式也尽量按照 ECMAScript® Language Specification 中的描述去实现。

阶段 1 : Tokenizer

Tokenizer 词法分析 (Lexical Analysis)，也就是常说的 分词 ，将要解析的源解析为逐个符合特定语言规则的符号，这个过程通过实现 DFA 做具体的分词工作

Lexer / Scanner 都是在描述这个阶段

实现分词的方式

根据语言的词法规则，标记出一串字符中的不同类型 Token

这里我们简单 parse 一个 stream：age ≥ 26

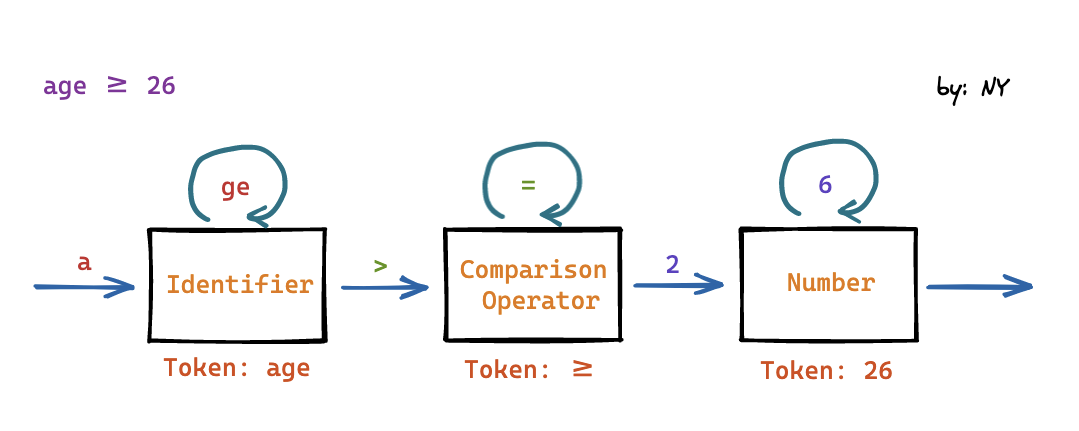
Identifier、Number、>= 都是终结符，终结符都是词法分析中产生的 Token。

而那些非叶子节点，就是非终结符。

文法的推导过程，就是把非终结符不断替换的过程，让最后的结果没有非终结符，只有终结符。

利用实现好的 DFA，在不同的状态进行转移，解析出 Token

• 完整的语法词法分析器只是一个具有完善状态和转移路线的 FSA
• 为了简化 Token 的解析，所以 Token 通常会采用正则文法（如名称、运算符、常量、注释）

为 Token 分配状态

在之后的 Parsing 过程中会经常使用到 判断当前 Token 是否符合一类定义的情况

比如: 判断当前 Token 是否为 Keyword 或者 Pattern

我们可以利用 位运算 进行状态的分配 (压缩状态)

在字符定义中，我们可以为字符配置特有的状态

/* Variable declaration */
VarKeyword = 71 | IsKeyword,
LetKeyword = 72 | IsKeyword,
ConstKeyword = 73 | IsKeyword,

LeftBrace = 12 | IsPatternStart, // {
LeftBracket = 19 | IsPatternStart | IsPropertyOrCallExpression, // [

// will match `{` and `[` or Keyword
if (parser.token & Token.IsPatternStart || parser.token & Token.IsKeyword) {
  // todo
}

判断 Keyword 的方式

语言都有各自的保留字，比如 let，function，true/false

查看了 Esprima 的谓词实现，觉得还可以有简约的实现

private isKeyword(id: string): boolean {
  switch (id.length) {
      case 2:
          return (id === 'if') || (id === 'in') || (id === 'do');
      case 3:
          return (id === 'var') || (id === 'for') || (id === 'new') ||
              (id === 'try') || (id === 'let');
      case 4:
          return (id === 'this') || (id === 'else') || (id === 'case') ||
              (id === 'void') || (id === 'with') || (id === 'enum');
            // ...
      default:
          return false;
  }
}

由于我们可以知道当前 Token 的字符值，这里简单使用了 HashMap 取值的方式：

function scanIdentifier(parser: IParserState): Token {
    // ...
    //
  return mapKeywordTable[parser.tokenValue] || Token.Identifier;
}

...
// Keyword hash-map Table
export const mapKeywordTable: { [key: string]: Token } = {
  this: { value: Token.ThisKeyword },
  function: { value: Token.FunctionKeyword },
  if: { value: Token.IfKeyword },
  return: { value: Token.ReturnKeyword },
  var: { value: Token.VarKeyword },
  else: { value: Token.ElseKeyword },
}

BTW: 正则判断并没有优势

阶段 2 : Parsing

Parsing 语法分析 (Syntactic Analysis)，在这个阶段将在 Tokenizer 的基础上进行语法结构的识别

Grater 采用的解析方式是常见的 LL(k) Parser，是一种 自顶向下的 Parser

其中两个 L 的意思分别是：Left-to-right , Leftmost derivation

语句的规则通常 左边是 非终结符(Non-terminal)，右边是 产生式(Production Rule)，这种表达方式是 上下文无关文法(Context-free grammar)，在解析的过程中，非终结符将被其产生式替换，直到最后全部变成 终结符(Terminal)，也就是 Token，这一系列的过程叫做 Derivation （Leftmost derivation 指总是先把左边的非终结符展开，也就是从最左的非终结符开始推导，而且是深度优先）

其中 Recursive Descent Parsing 的实现其实很简单，非常的直观

实际上，JS 语法并不是完全纯粹的 Context-free grammar

而递归下降的实现里可以做到超越 CFG，在 Recursion func 中可以传递 context，在有需要上下文解析的情况里用到，以及丰富错误信息

消除左递归 left recursion

由于 Grater 是没有 Backtracking，那么就需要分析时对每个文法做正确的展开

但遇到左递归的文法，就会有问题，解决的方法通常是将左递归转化为等价的右递归形式

例如在 Binary Expression 的词法规则中，产生式的第一个元素是它自身，那么程序就会无限地递归下去，这种情况就叫做左递归。

比如 加法表达式的产生式中有一条是 “加法表达式 + 乘法表达式”

我们用 2 + 3 这个加法表达式来举例

ECMAScript Language Specification 中加法表达式的定义式:

AdditiveExpression

• MultiplicativeExpression
• AdditiveExpression + MultiplicativeExpression
• AdditiveExpression - MultiplicativeExpression

MultiplicativeExpression

• ExponentiationExpression
• MultiplicativeExpression MultiplicativeOperator ExponentiationExpression

接下来，我们只保留关键信息，简化的 BNF :

Additive: Multiplicative | (Additive + Multiplicative);

Multiplicative: IntLiteral | (Multiplicative * IntLiteral);

非终结符通常只用了一个大写字母代表，通常可简写为：

A -> M
   | A + M
   | A - M

我们的 Token 串是 2 + 3，来进行匹配规则

1. 应用第一条规则 A -> M，2 + 3 不是 M 表达式，转移到使用 A -> A + M 的方法匹配
2. A + M 将从 A 开始推导，重复了第一步的操作，导致了 infinite loop

• 如果对第二个步骤不理解，比如认为 2+3 应该符合 A + M 这个规则
  
  这样认为是因为本能的使用了广度优先，而我们的 Parser 是依照深度优先

然后可以通过转换文法消除左递归

A: M | M + A

再进行推导就消除了之前的循环

其实 左递归的问题 与 运算符优先级也有关联

Operator Precedence 运算符优先级

优先级是通过在语法推导中的层次来决定的：优先级越低的，越先尝试推导。

而对应在 AST 树中，层次越深，优先级越高

例如：1 + 2 * 3 产生的 AST 结构为

{
  "type": "Program",
  "sourceType": "script",
  "body": [
    {
      "type": "ExpressionStatement",
      "expression": {
        "type": "BinaryExpression",
        "left": {
          "type": "Literal",
          "value": 1
        },
        "right": {
          "type": "BinaryExpression",
          "left": {
            "type": "Literal",
            "value": 2
          },
          "right": {
            "type": "Literal",
            "value": 3
          },
          "operator": "*"
        },
        "operator": "+"
      }
    }
  ]
}

Grater 采用 Precedence climbing method 实现高效的运算符优先级解析。

如果当前运算符的优先级小于前一个运算符，则提前返回叶子节点。并将 高优先级运算符 左右两边的节点合并为一个 BinaryExpression

还有几个特殊的情况需要处理：

1. 括号优先于所有运算符
2. ^ 是右关联的，而所有其他二进制运算符是左关联的

这里提及两个解决优先级相关的算法

1. Precedence climbing
2. Shunting-yard algorithm

Conclusion

如果你有想法打算尝试写一个 Parser，我的建议是 Just write it，你可以先不用管那些固有理论，着手去实现它，在实现过程中不断优化，遇到问题再依据理论加以解决

Sometimes you gotta run before you can walk — Iron Man

Contribution

为 Grater 实现更多的功能及识别更多的语法

如果你有兴趣贡献代码給 Grater，让它变成更完善的 Parser，非常欢迎结合你的思考来实现 Grater 目前所需的功能点，在这里可以查看

Reference

1. Acorn: Alternative, faster React.js JSX parser
2. Operator-precedence parser
3. LR parser
4. LL parser
5. Top-down parsing
6. Recursive descent parser
7. Left recursion
8. NFA
9. Context-free grammar